Pixel Dungeon's Level Generation
Pixel Dungeon is an addicting open-source roguelike that was developed for Android in late 2014 and has spawned multiple forks, the most notable being Shattered Pixel Dungeon which continues to be updated today. In this post, I’m mostly interested in examining how level is generated so I’ve given the source code a read and attempt to explain it from a bottom-up approach.
Room generations mostly revolves around the subdivision of a rectangle into smaller rectangles
until the subdivision goal is satisfied. In general the goal can be stated as follows, we want the maximum
size dimensions of a rectangle to be (maxRoomSize, maxRoomSize). If a rectangle satisfies this constraint then there is
a chance it will be added to a set of rooms and if it is not added the rectangle is split again. The chance of adding the rectangle
is minRoomSize * minRoomSize / roomArea. Thus when a rectangle has dimension less than (minRoomSize, minRoomSize) the probability of
adding it is 1. This ensures that the split function will terminate.
Here is an animated image of the subdivision algorithm and its final result.

Additonaly here is a little demo which allows you to step through each split.
Subdivision results in a collection of rectangles with varying sizes which are then
transformed into rooms. A room has a dimension (it’s rectangle), a type, a collection
of neighbours, and a collection of connected rooms.
Two rooms are considered neighbours if they share wall with length greater than 3 and
a room can only be connected to a neighbour. A collection of rooms is considered a level, which
can have an entrance and exit. The entrance and exit are randomly placed but their placements may be rejected if
they do not satisfy certain criteria. In particular the room distance between the entrance and
exit must be greater than the square root of total rooms. If this criteria is not satisfied after a small number of iterations,
the entire level is rejected.
Once the entrance and exit are placed the shortest path between them is calculated and connected, which ensures the level can be completed. After this path is calculated the weight of all the rooms along this path have their weights set to the total cost of the just calculated path, then the shortest path is calculated again, which provides multiple routes for completing a level. However, the player will have a linear path from the entrance to the exit and will be unlikely to backtrack.
To add some backtracking, a goal of how many rooms we want to include. This is determined by the expresion
Random(0.5, 0.7) * numRooms. While the number of connected rooms is less than this goal, randomly select a connected room
and one of its neighbours. If the neighbour is not included in the level then connect them, otherwise don’t.
Repeat this until the goal is reached.
When the connected goal is reached, assign a type to all rooms. The default
type of a room is EMPTY which is invalid for any connected room. The non-empty
rooms types are STANDARD and TUNNEL.
Here is a demo and some pictures that show you a sample of the levels that can be generated.
The room with the blue outline contains the entrance and the green outline represents the exit.
Also, only EMPTY and STANDARD rooms exists
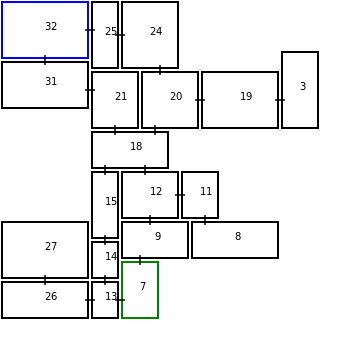
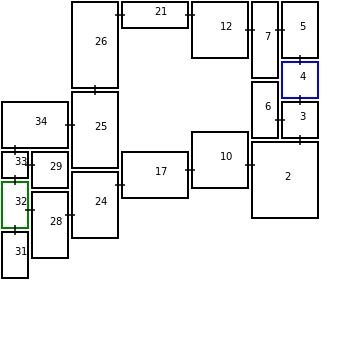
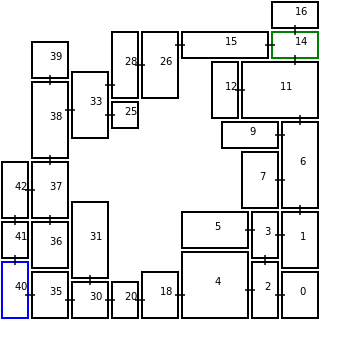
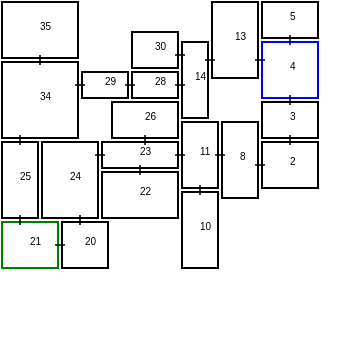
The levels generated so far are bland and are all rectangular. Pixel Dungeon solves this with the use of Painters. Painters apply specialized styling dependent on the room type, so a tunnel room would have a painter responsible for digging out tunnels, while other painters may add bookshelves, collapse floors, or turn the room’s rectangular shape into something else. Note that painters don’t operate on the graph structures but instead transform it into a tileset, which allows for a finer level of detail.
This is the general process behind Pixel Dungeon’s level generations, character is added with additional rooms types, painters, and different textures depending on the dungeon depth. Overall this process provides a great starting point if you wish to develop your own rouge-like maps.